数组

Array 数组

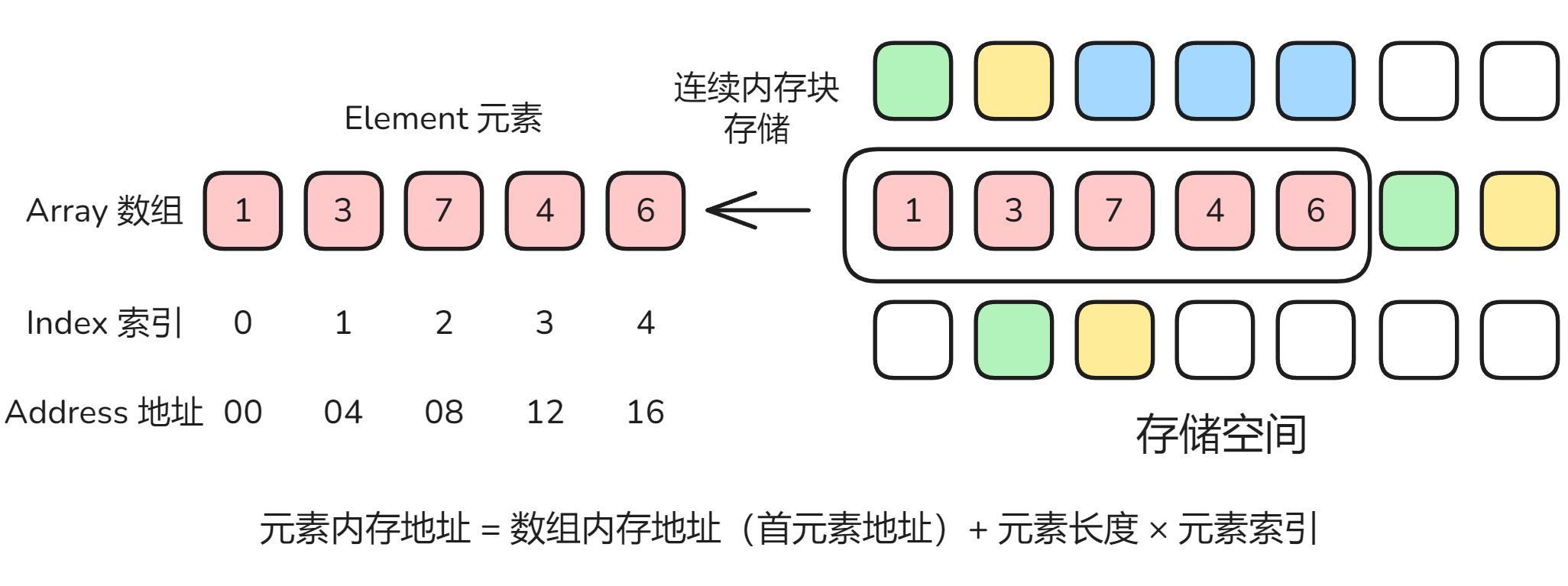
数组是一种线性数据结构。其将相同类型的元素存储在连续的内存空间中。我们将元素在数组中的位置称为该元素的索引 Index。

一、数组的操作

数组元素被存储在连续的内存空间中，这意味着计算数组元素的内存地址非常容易。索引本质上是内存地址的偏移量，一般编程语言首个元素的地址偏移量为 0。

1. 初始化数组

在大多数编程语言中，初始化数组时需要指定其大小或提供初始元素。一旦初始化，数组的长度通常是固定的。

python

# 初始化一个空数组
empty_array = []

# 初始化一个包含预设元素的数组
numbers = [1, 2, 3, 4, 5]

# 初始化一个指定大小并填充默认值的数组
# Python中通常通过列表推导式实现，因为Python列表是动态数组
zeros = [0] * 5 # [0, 0, 0, 0, 0]

# 在C++中初始化固定大小数组
// int static_array[5]; // 声明一个包含5个整数的数组
// int initialized_array[5] = {1, 2, 3, 4, 5}; // 声明并初始化

2. 访问元素

数组支持在 $O (1)$ 时间内随机访问任意一个元素，这是其主要优势之一。

python

numbers = [10, 20, 30, 40, 50]

# 访问第一个元素 (索引为0)
first_element = numbers[0] # 10
print(f"第一个元素: {first_element}")

# 访问第三个元素 (索引为2)
third_element = numbers[2] # 30
print(f"第三个元素: {third_element}")

# 修改元素
numbers[1] = 25
print(f"修改后的数组: {numbers}") # [10, 25, 30, 40, 50]

3. 插入元素

由于数组的连续存储特性，在数组中间插入一个元素需要将该位置及之后的所有元素都向后移动一位，为新元素腾出空间。如果数组已满，则可能需要扩容。

python

def insert_element(arr, index, value):
    if index < 0 or index > len(arr): # Python列表是动态的，这里模拟固定数组行为
        print("索引越界")
        return arr
    
    # 模拟固定大小数组的插入，会覆盖末尾元素
    new_arr = [0] * len(arr)
    for i in range(index):
        new_arr[i] = arr[i]
    new_arr[index] = value
    for i in range(index, len(arr) - 1):
        new_arr[i+1] = arr[i]
    return new_arr

my_array = [1, 2, 3, 4, 5]
print(f"原数组: {my_array}")
# 在索引2处插入99
my_array = insert_element(my_array, 2, 99)
print(f"插入后的数组: {my_array}") # [1, 2, 99, 3, 4] (5被挤出)

# Python列表的内置插入方法 (动态扩容)
python_list = [1, 2, 3]
python_list.insert(1, 99) # 在索引1处插入99
print(f"Python列表插入后: {python_list}") # [1, 99, 2, 3]

4. 删除元素

若想删除索引 $i$ 处的元素，则需要把索引 $i$ 之后的元素都向前移动一位，覆盖被删除的元素。

python

def delete_element(arr, index):
    if index < 0 or index >= len(arr):
        print("索引越界")
        return arr
    
    new_arr = [0] * (len(arr) - 1) # 模拟删除后数组长度减1
    for i in range(index):
        new_arr[i] = arr[i]
    for i in range(index + 1, len(arr)):
        new_arr[i-1] = arr[i]
    return new_arr

my_array = [1, 2, 99, 3, 4]
print(f"原数组: {my_array}")
# 删除索引2处的元素 (99)
my_array = delete_element(my_array, 2)
print(f"删除后的数组: {my_array}") # [1, 2, 3, 4]

# Python列表的内置删除方法
python_list = [1, 99, 2, 3]
del python_list[1] # 删除索引1处的元素
print(f"Python列表删除后: {python_list}") # [1, 2, 3]

数组的插入与删除操作有以下缺点：

时间复杂度高：数组的插入和删除的平均时间复杂度均为 $O (N)$ ，其中 $N$ 为数组长度，因为需要移动大量元素。
丢失元素：对于固定长度数组，插入元素可能导致末尾元素丢失。
内存浪费：如果数组分配的大小超过实际所需，那么多余的空间就被浪费了。

5. 遍历数组

既可以通过索引遍历数组，也可以直接遍历获取数组中的每个元素。

python

colors = ["red", "green", "blue"]

# 通过索引遍历
print("通过索引遍历:")
for i in range(len(colors)):
    print(f"索引 {i}: {colors[i]}")

# 直接遍历元素
print("\n直接遍历元素:")
for color in colors:
    print(color)

6. 查找元素

在数组中查找指定元素需要遍历数组，每轮判断元素值是否匹配，若匹配则输出对应索引。因为数组是线性数据结构，所以上述查找操作被称为“线性查找”。

python

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i # 找到目标，返回索引
    return -1 # 未找到

my_list = [10, 20, 30, 40, 50]

index1 = linear_search(my_list, 30)
print(f"30 的索引是: {index1}") # 2

index2 = linear_search(my_list, 99)
print(f"99 的索引是: {index2}") # -1

7. 扩容数组

在大多数编程语言中，数组的长度是不可变的。扩容数组则需重新建立一个更大的数组，然后把原数组元素依次复制到新数组。这是一个 $O (N)$ 的操作，在数组很大的情况下非常耗时。

python

def resize_array(arr, new_capacity):
    if new_capacity < len(arr):
        print("新容量不能小于当前元素数量")
        return arr
    
    new_arr = [0] * new_capacity # 创建一个新数组
    for i in range(len(arr)):
        new_arr[i] = arr[i] # 复制旧数组元素到新数组
    return new_arr

my_array = [1, 2, 3]
print(f"原数组容量: {len(my_array)}, 数组: {my_array}")

# 扩容到6
my_array = resize_array(my_array, 6)
print(f"扩容后容量: {len(my_array)}, 数组: {my_array}") # [1, 2, 3, 0, 0, 0]

二、优点与局限性

数组存储在连续的内存空间内，且元素类型相同。这种做法包含丰富的先验信息，系统可以利用这些信息来优化数据结构的操作效率。

1. 优点

空间效率高：数组为数据分配了连续的内存块，无须额外的结构开销。
支持随机访问：数组允许在 $O (1)$ 时间内访问任何元素，通过索引直接计算内存地址。
缓存局部性：当访问数组元素时，计算机不仅会加载它，还会缓存其周围的其他数据，从而借助高速缓存来提升后续操作的执行速度。

2. 局限性

连续空间存储是一把双刃剑，其存在以下局限性。

插入与删除效率低：当数组中元素较多时，插入与删除操作需要移动大量的元素，平均时间复杂度为 $O (N)$ 。
长度不可变：数组在初始化后长度就固定了，扩容数组需要将所有数据复制到新数组，开销很大。
空间浪费：如果数组分配的大小超过实际所需，那么多余的空间就被浪费了。

三、数组典型应用

数组是一种基础且常见的数据结构，既频繁应用在各类算法之中，也可用于实现各种复杂数据结构。

随机访问：如果我们想随机抽取一些样本，那么可以用数组存储，并生成一个随机序列，根据索引实现随机抽样。
排序和搜索：数组是排序和搜索算法最常用的数据结构。快速排序、归并排序、二分查找等都主要在数组上进行。
查找表：当需要快速查找一个元素或其对应关系时，可以使用数组作为查找表。假如我们想实现字符到 ASCII 码的映射，则可以将字符的 ASCII 码值作为索引，对应的元素存放在数组中的对应位置。
机器学习：神经网络中大量使用了向量、矩阵、张量之间的线性代数运算，这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。
数据结构实现：数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如，图的邻接矩阵表示实际上是一个二维数组。

四、编程语言中的具体实例

数据结构
 栈
 队列
 哈希表
 堆
 图
 快速排序
 归并排序
 二分查找
 查找表