四元数

Quaternion
是爱尔兰数学家威廉·哈密顿在1843年发明的一种数学概念，是复数的自然推广。

复数将实数轴扩展到了二维平面
而四元数则将复数系扩展到了四维空间

一种数学上的代数结构，用于在三维空间中表示旋转和方向。

欧拉角描述旋转的结果
四元数描述旋转的过程

一、基本定义

一个四元数 $q$ 可以表示为一个有序实数组 $(w, x, y, z)$ ，或者更常见的形式：

\begin{array}{r} q = w + x i + y j + z k \end{array}

其中 $w, x, y, z$ 是实数，而 $i, j, k$ 是三个虚数单位。

$w$ 被称为四元数的实部或标量部。
$v = (x, y, z)$ 被称为虚部或向量部。^[1]

实数轴和三个虚轴都相互垂直，符合右手定则：

\begin{array}{r} i^{2} = j^{2} = k^{2} = i j k = - 1 \end{array}

由这个核心规则可以推导出它们之间的乘法关系：单位四元数的乘法表示四维空间的双旋转

\begin{matrix} i j = k, j k = i, k i = j \\ j i = - k, k j = - i, i k = - j \end{matrix}

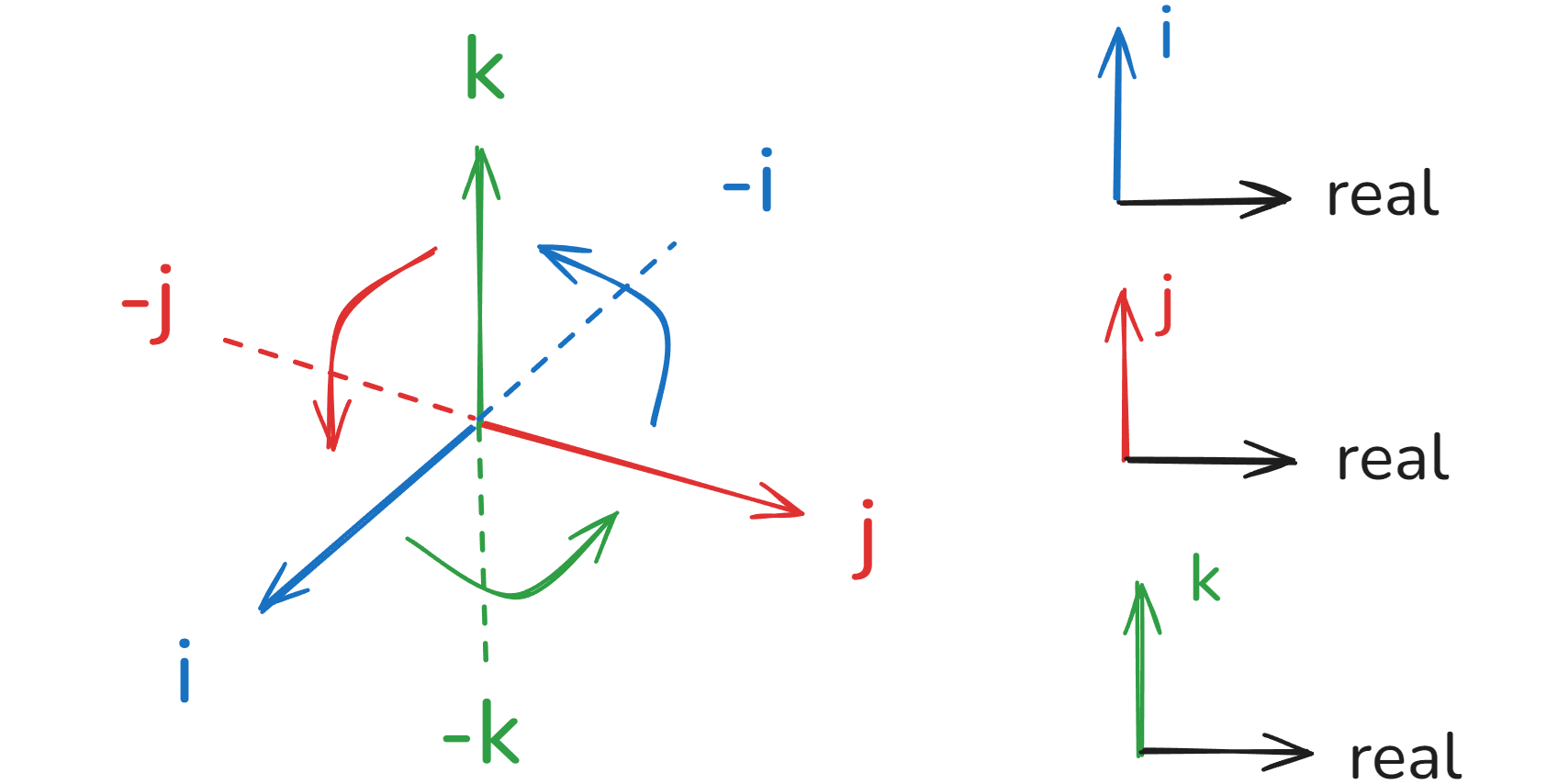
以虚数 $i$ 为例， $i$ 的作用相当于将 $j k$ 平面上的向量逆时针旋转 $90^{\circ}$

i j = k, i k = - j, i (- j) = - k, i (- k) = j

而 $i$ 如果作用于 $i$ 本身，则进入实数范围 $i^{2} = - 1$

对于四元数中一般的单位向量 $v$ ， $v$ 左乘，相当于将与 $v$ 垂直的平面逆时针旋转 $90^{\circ}$ ，而将沿着 $v$ 的分量将进入实数范围，跑出三维虚空间

q = \cos θ + v \sin θ q^{- 1} = \cos θ - v \sin θ

任意一个向量在三维空间中绕向量 $v$ 旋转 $2 θ$ 角： $x^{'} = q x q^{- 1}$

二、基本运算

设有两个四元数 $q_{1} = w_{1} + x_{1} i + y_{1} j + z_{1} k$ 和 $q_{2} = w_{2} + x_{2} i + y_{2} j + z_{2} k$ 。

加法: 各分量相加

q_{1} + q_{2} = (w_{1} + w_{2}) + (x_{1} + x_{2}) i + (y_{1} + y_{2}) j + (z_{1} + z_{2}) k

乘法: 利用分配律和虚数单位的乘法规则展开。如果用向量部表示 $q_{1} = (w_{1}, \vec{v_{1}})$ 和 $q_{2} = (w_{2}, \vec{v_{2}})$ ，乘法可以更紧凑地表示为：（其中 $\cdot$ 是点积， $\times$ 是叉积）

q_{1} q_{2} = (w_{1} w_{2} - \vec{v_{1}} \cdot \vec{v_{2}}, w_{1} \vec{v_{2}} + w_{2} \vec{v_{1}} + \vec{v_{1}} \times \vec{v_{2}})

共轭 (Conjugate): 将虚部取反

q^{*} = w - x i - y j - z k

范数 (Norm)：定义为

| q | = \sqrt{w^{2} + x^{2} + y^{2} + z^{2}} | q_{1} q_{2} | = | q_{1} | | q_{2} | 。

逆 (Inverse): 对于非零四元数 $q$ ，其逆为

q^{- 1} = \frac{q^{*}}{| q |^{2}}

三、用四元数表示旋转

复数乘除法的几何意义是来描述二维的旋转，乘以一个复数，复数的模表示伸缩，复数的角度表示顺时针的旋转角度：如果想要将一个向量 $x + i y$ 顺时针旋转 $θ$ 角，只需要乘以模为 1 的向量 $\cos θ + i \sin θ$ ，得到旋转后的向量 $(\cos θ + i \sin θ) (x + i y)$

四元数描述三维的旋转类似，向量 $p = (x_{1} i, y_{1} j, z_{1} k)$ , 四元数 $q = w_{0} + x_{0} i + y_{0} j + z_{0} k$

\begin{array}{r} q p q^{- 1} = (w_{0} + x_{0} i + y_{0} j + z_{0} k) (x_{1} i, y_{1} j, z_{1} k) (w_{0} - x_{0} i - y_{0} j - z_{0} k) \end{array}

这是四元数最重要的应用。三维空间中的一个旋转操作可以通过一个单位四元数 (Unit Quaternion) 来表示。单位四元数是指范数为 1 的四元数，即 $| q | = 1$ 。

一个绕单位向量轴 $\vec{u} = (u_{x}, u_{y}, u_{z})$ 旋转角度 $θ$ 的操作，可以由以下单位四元数 $q$ 表示：

q = (\cos \frac{θ}{2}, \sin \frac{θ}{2} \vec{u}) = \cos \frac{θ}{2} + (u_{x} \sin \frac{θ}{2}) i + (u_{y} \sin \frac{θ}{2}) j + (u_{z} \sin \frac{θ}{2}) k

要将这个旋转应用于空间中的一个点（或向量） $\vec{p} = (p_{x}, p_{y}, p_{z})$ ，我们首先将 $\vec{p}$ 表示为一个纯四元数（实部为 0） $p = 0 + p_{x} i + p_{y} j + p_{z} k$ 。

旋转后的点 $p^{'}$ 通过以下“三明治”乘法计算得到：

p^{'} = q p q^{- 1}

计算结果 $p^{'}$ 的实部将为 0，其虚部就是旋转后的向量坐标。

直观化展示：https://eater.net/quaternions

四、优点与应用

与欧拉角和旋转矩阵相比，使用四元数表示旋转有几个关键优势：

避免万向节死锁 (Gimbal Lock): 这是欧拉角表示法的一个致命缺陷，而四元数不存在这个问题。
计算效率高: 四元数乘法比矩阵乘法需要更少的计算量。
存储紧凑: 只需要 4 个浮点数，而 $3 \times 3$ 旋转矩阵需要 9 个。
平滑插值: 可以使用球面线性插值 (Slerp) 在两个旋转之间进行平滑、自然的插值，这在动画和机器人轨迹规划中非常有用。

由于这些优势，四元数被广泛应用于：

计算机图形学和游戏引擎 (如 Unity, Unreal Engine)
机器人学和无人机姿态控制
航空航天器导航

四元数在计算机图形学、机器人学、航天器姿态控制等领域有广泛应用，因为它们可以方便地进行旋转的插值（Slerp）和避免万向节锁（Gimbal Lock）问题。

五、与李群的关系

所有单位四元数的集合在四元数乘法下构成一个群，这个群同构于特殊酉群 $S U (2)$ 。存在一个 2 对 1 的满群同态从单位四元数群（或 $S U (2)$ ）到三维旋转群特殊正交群 $S O (3)$ 。这揭示了三维旋转与量子力学中自旋 1/2 粒子（由 $S U (2)$ 描述）的深刻数学联系。

Vector 的名词在此首次提出，不过现代意义主要指向量 ↩︎