降维

Dimensionality Reduction
将训练数据中的样本 (实例) 从高维空间转换到低维空间，该过程与信息论中有损压缩概念密切相关。（不存在完全无损的降维）

降维概述

维数灾难(Curse of Dimensionality)：涉及数字分析、抽样、组合、机器学习、数据挖掘和数据库等诸多领域。通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。维度太大也会导致机器学习性能的下降，并不是特征维度越大越好，模型的性能会随着特征的增加先上升后下降。

主要作用

减少冗余特征，降低数据维度（去掉冗余特征对机器学习的计算结果不会有影响）
数据可视化。（t-SNE：将数据点之间的相似度转换为概率。原始空间中的相似度由高斯联合概率表示，嵌入空间的相似度由“t分布”表示，关注数据的局部结构）

降维的优点：减少特征的维数，减少了特征维数所需的计算训练时间；数据集特征的降维有助于快速可视化数据；通过处理多重共线性消除冗余特征。
降维的缺点：降维可能会丢失一些数据；主成分分析，需要考虑多少主成分是难以确定的，往往使用经验法则

为什么需要降维？

维度灾难 (Curse of Dimensionality):
- 在高维空间中，数据会变得极其稀疏，导致样本点之间的距离变得几乎相等，使得许多机器学习算法（特别是依赖距离度量的算法，如 K近邻、支持向量机）的性能急剧下降。
- 训练模型所需的样本数量呈指数级增长。
可视化: 人类只能直观地理解二维或三维数据。降维可以将高维数据投影到低维空间，便于数据可视化和模式发现。
去噪: 降维可以去除数据中的噪声和冗余信息，保留最重要的特征，从而提高模型的鲁棒性。
减少存储和计算成本: 降低数据维度可以显著减少存储空间和模型训练、推理所需的计算时间。

奇异值分解 SVD

Singular Value Decomposition SVD

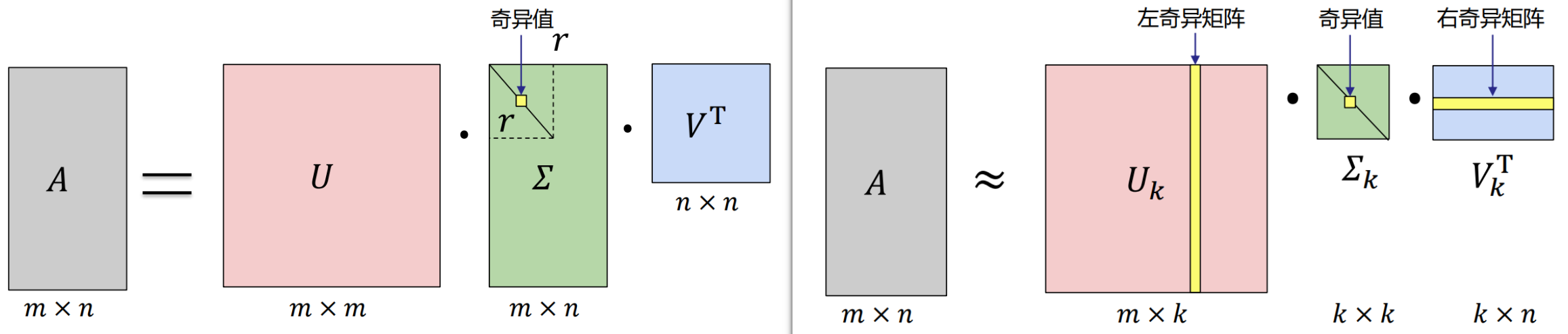
SVD可以将一个矩阵 A 分解为三个矩阵的乘积：正交矩阵 $U, V^{T}$ ，对角矩阵 $Σ$

\begin{array}{r} A = U Σ V^{T} \end{array}

$(A A^{T}) u_{i} = λ_{i} u_{i}$ $U$ 矩阵中每个列向量为左奇异向量
$(A^{T} A) v_{i} = λ_{i} v_{i}$ $V$ 矩阵中每个列向量为右奇异向量
$σ_{i} = \sqrt{λ_{i}}$ 为奇异值，对角矩阵对角线上的奇异值递减排列

主成分分析 PCA

Principal Component Analysis PCA
基本思想：减少数据集的特征数量，同时尽可能地保留信息：将一个大的特征集转换成一个较小的特征集，这个特征集仍然包含了原始数据中的大部分信息，从而降低了原始数据的维数。

两种实现方法

基于SVD分解协方差矩阵实现PCA算法
基于特征值分解协方差矩阵实现PCA算法

第一步：均值归一化，计算出所有特征的均值 $x_{j} = x_{j} - μ_{j}$
第二步：计算协方差矩阵 $Σ = \frac{1}{n} \sum_{i = 1}^{n} (x_{i} x_{i}^{T})$
第三步：计算协方差矩阵的特征值和特征向量
对特征值从大到小排序，选择其中最大的 k个。然后将其对应的 k 个特征向量分别作为行向量组成特征向量矩阵 $P$

计算实例

求 $A = (\begin{matrix} 1 & 2 & 0 \\ 2 & 0 & 2 \end{matrix})$ 的奇异值分解。
因为 $A$ 的秩为 2，所以最多有两个特征值，计算 $A A^{T}$ 的特征值，即可得到 $Σ$

\begin{array}{r} A A^{T} = (\begin{array}{c} 5 & 2 \\ 2 & 8 \end{array}) | λ I - A A^{T} | = (λ - 4) (λ - 9) \end{array}

$A A^{T}$ 有特征值 $λ_{1} = 9, λ_{2} = 4$ ，则 $A^{T} A$ 有特征值 $λ_{1} = 9, λ_{2} = 4, λ_{3} = 0$
$(λ I - A A^{T}) \vec{p} = \vec{0}$ 计算特征向量，作为矩阵 $U$ 的列向量
$(λ I - A^{T} A) \vec{p} = \vec{0}$ 计算特征向量，作为矩阵 $V$ 的列向量
（注意均将特征向量归一化为单位向量！！！）

\begin{array}{r} U = \frac{1}{\sqrt{5}} (\begin{array}{c} 1 & - 2 \\ 2 & 1 \end{array}) V = \frac{1}{3 \sqrt{5}} (\begin{array}{c} 5 & 0 & - 2 \sqrt{5} \\ 2 & 6 & \sqrt{5} \\ 4 & - 3 & 2 \sqrt{5} \end{array}) \end{array}

奇异值为特征值开根号，降序排列： $σ_{1} = \sqrt{9} = 3 σ_{2} = \sqrt{4} = 2$

\begin{array}{r} Σ = (\begin{array}{c} 3 & 0 & 0 \\ 0 & 2 & 0 \end{array}) A = U Σ V^{T} \end{array}

Dimensionality Reduction

降维是机器学习中一种重要的无监督学习技术，旨在将高维数据（即具有大量特征的数据）映射到低维空间，同时尽可能地保留数据中的重要信息（如结构、模式或区分性）。

两大类降维方法

降维方法主要分为两类：

特征选择 (Feature Selection):
- 原理: 从原始特征集中直接选择一个最有代表性的子集，丢弃不相关的或冗余的特征。
- 特点: 保留了原始特征的物理意义，可解释性强。
- 方法: 特征工程中的过滤法、包装法、嵌入法。
特征提取 (Feature Extraction):
- 原理: 将原始特征通过某种变换或组合，生成一组全新的、更低维的特征。这些新特征通常是原始特征的线性或非线性组合。
- 特点: 可能会失去原始特征的物理意义，但通常能更有效地压缩信息。

常见降维算法

1. 线性降维

主成分分析 (Principal Component Analysis, PCA)
- 原理: PCA 是一种最常用的线性降维方法。它通过正交变换将原始数据投影到一组新的正交坐标轴上，这些新坐标轴被称为主成分 (Principal Components)。第一个主成分捕获数据中最大的方差，第二个主成分捕获剩余方差中最大的部分，以此类推。
- 目标: 寻找一个低维子空间，使得数据投影到该子空间后，方差最大化（即保留最多的信息）。
- 数学基础: 基于数据的协方差矩阵进行特征值分解。
- 优缺点:
  - 优点: 简单、高效、易于理解；能有效去除冗余特征。
  - 缺点: 只能进行线性降维；对异常值敏感；新特征（主成分）的可解释性较差。
线性判别分析 (Linear Discriminant Analysis, LDA)
- 原理: LDA 是一种有监督的降维方法（尽管它通常被归类在降维算法中）。它旨在找到一个投影方向，使得投影后类间散度最大化，同时类内散度最小化。
- 目标: 最大化类别之间的可分离性。
- 适用场景: 分类任务的预处理，当需要强调类别区分度时。

2. 非线性降维

t-SNE (t-Distributed Stochastic Neighbor Embedding)
- 原理: 一种强大的非线性降维技术，特别适用于高维数据的可视化。它旨在将高维数据点映射到二维或三维空间，同时尽可能地保留数据点之间的局部结构（即高维空间中相近的点在低维空间中也相近）。
- 特点: 能够揭示数据中复杂的非线性结构和簇；计算成本高，不适合用于降维后进行其他机器学习任务。
- 适用场景: 数据探索、可视化、聚类结果的展示。
自编码器 (Autoencoder)
- 原理: 一种神经网络模型，通过无监督学习的方式，将输入数据编码成一个低维的潜在表示（编码器），然后再从这个潜在表示解码重构出原始输入（解码器）。中间的潜在表示就是降维后的结果。
- 特点: 能够学习到数据的非线性特征表示；可以用于去噪和生成。
- 适用场景: 图像、文本等复杂数据的特征学习和降维。