聚类

Clustering

聚类是机器学习中一种重要的无监督学习任务。其目标是根据数据样本之间的相似性或距离，将数据集中的样本划分为若干个簇 (Clusters)，使得同一簇内的样本相似度高，而不同簇之间的样本相似度低。

聚类算法的性能高度依赖于如何定义样本之间的“相似性”或“距离”。距离度量

聚类与分类的对比

聚类 (Clustering): 无监督学习。数据没有预先定义的标签。算法的任务是发现数据中固有的结构，将相似的样本自动分组。
分类 (Classification): 有监督学习。数据有预先定义的类别标签。算法的任务是学习一个映射函数，将新样本分配到已知的类别中。

一、基于划分的聚类 (Partitioning-based Clustering)

这类算法将数据划分为预先指定数量的簇，每个簇代表一个数据子集。

K-Means
原理: 迭代地将数据点分配到最近的簇中心，然后重新计算簇中心，直到收敛。
目标函数: 最小化所有数据点到其所属簇中心的平方距离之和（簇内平方和）。

J = \sum_{j = 1}^{K} \sum_{x_{i} \in C_{j}} ∥ x_{i} - μ_{j} ∥^{2}

其中 $K$ 是簇的数量， $C_{j}$ 是第 $j$ 个簇， $μ_{j}$ 是第 $j$ 个簇的中心。

算法步骤:

初始化: 随机选择 $K$ 个数据点作为初始簇中心。
分配: 将每个数据点分配到距离其最近的簇中心。
更新: 重新计算每个簇的中心（通常是簇内所有点的均值）。
迭代: 重复步骤2和3，直到簇中心不再变化或达到最大迭代次数。

优缺点:
优点: 简单、高效，适用于大规模数据集。
缺点: 需要预先指定 $K$ 值；对初始中心敏感；容易陷入局部最优；对噪声和异常值敏感；只能发现球形簇。
K-Medoids (PAM): K-Means的变体，使用簇内实际数据点作为中心（medoid），对异常值更鲁棒。
具有一个迭代过程，数据集被分组成若干个预定义的不重叠的聚类或子组，数据点分配给簇，以便簇的质心和数据点之间的平方距离之和最小，在这个位置，簇的质心是簇中数据点的算术平均值

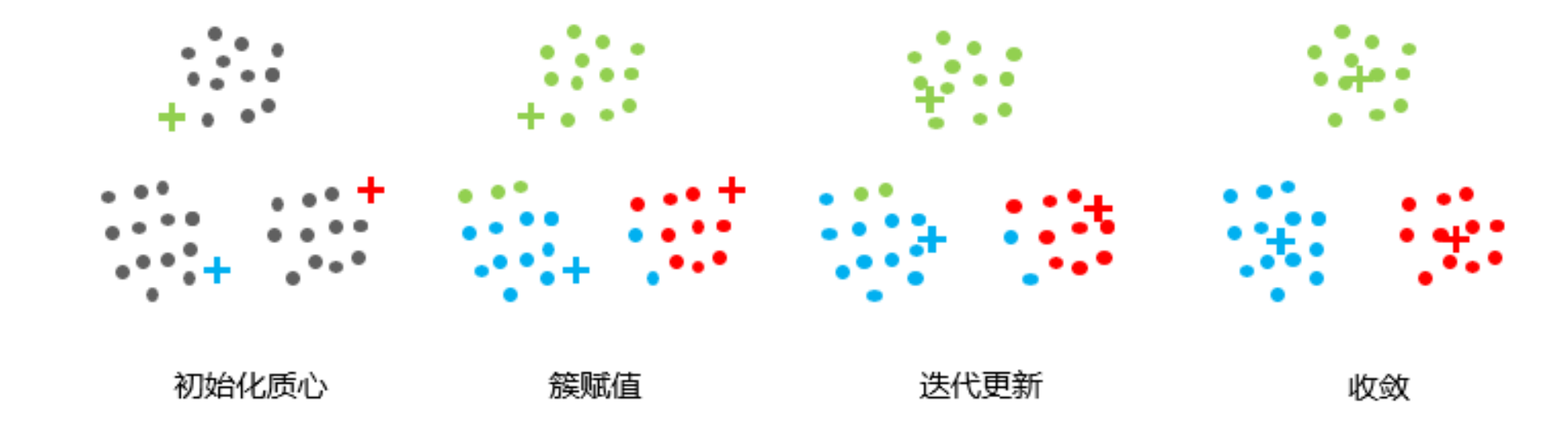
算法流程：

选择 K 个点作为初始质心。（簇的质心必须小于训练数据点的数目）
将每个点指派到最近的质心，形成 K 个簇。（遍历所有数据点，计算所有质心与数据点之间的距离，簇将根据与质心的最小距离而形成）
对于上一步聚类的结果，进行平均计算，得出该簇的新的聚类中心。（迭代地将质心移动到一个新位置。取一个簇的数据点，计算它们的平均值，然后将该簇的质心移动到这个新位置。对所有其他簇重复相同的步骤。）
重复上述两步/直到迭代结束：质心不发生变化。（直到质心停止移动，即它们不再改变自己的位置，收敛。）

肘部法则选择 K 值：肘点之前代价函数的值会迅速下降，肘点之后代价函数的值会就下降得非常慢。一般选择肘点。（比较多次运行 K-均值的结果，选择代价函数最小的结果）

优点：原理比较简单，实现也是很容易，收敛速度快；聚类效果较优；可解释度比较强；要调参的参数仅仅是簇数 K
缺点：需要预先指定簇的数量；无法处理异常值和噪声数据；不适用于非线性数据集；高度重叠的数据，那么它就不能被区分；随机选择质心结果不理想；欧几里德距离可以不平等的权重因素，限制了能处理的数据变量的类型；

二、基于密度的聚类 (Density-based Clustering)

这类算法根据数据点的密度来发现任意形状的簇，并能识别噪声点。

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
- 原理: 基于两个参数： $ϵ$ （邻域半径）和 $M i n P t s$ （最小点数）。它将数据点分为三类：
  - 核心点 (Core Point): 在其 $ϵ$ 邻域内至少有 $M i n P t s$ 个点。
  - 边界点 (Border Point): 在其 $ϵ$ 邻域内点的数量少于 $M i n P t s$ ，但它位于某个核心点的 $ϵ$ 邻域内。
  - 噪声点 (Noise Point): 既不是核心点也不是边界点。
- 优缺点:
  - 优点: 能发现任意形状的簇；能有效识别噪声点；无需预先指定簇的数量。
  - 缺点: 参数选择困难；对密度不均匀的数据集效果不佳；不适用于高维数据。

Density-Based Spatial Clustering of Applications with Noise
如果 S 中任两点的连线内的点都在集合 S 内，那么集合 S 称为凸集。反之，为非凸集

基于密度的聚类算法：将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。

使用两个超参数：扫描半径 (eps) 和最小包含点数 (minPts) 来获得簇的数量：

扫描半径 eps : 用于定位点/检查任何点附近密度的距离度量，即扫描半径。
最小包含点数 minpts ：聚集在一起的最小点数（阈值），该区域被认为是稠密的
密度定义为：空间中任意一点的密度是以该点为圆心，以扫描半径构成的圆区域内包含的点数目

将数据点分为三类

核心点：在半径 Eps 内含有超过 MinPts 数目的点。
边界点：在半径 Eps 内点的数量小于 MinPts, 但是落在核心点的邻域内的点。
噪音点：既不是核心点也不是边界点的点。

算法流程：

将所有点标记为核心点、边界点或噪声点；（对每个点计算其扫描半径 Eps 的点的集合，如果集合内个数大于 MinPts，称为核心点；查看剩余点是否在核点的邻域内，若在，则为边界点，否则为噪声点。）
如果选择的点是核心点，则找出所有从该点出发的密度可达对象形成簇；（将距离不超过 Eps 的点相互连接，构成一个簇）
如果该点是非核心点，将其指派到一个与之关联的核心点的簇中；
重复以上步骤，直到所点都被处理过

三、基于层次的聚类 (Hierarchical-based Clustering)

这类算法通过构建一个嵌套的簇结构（树状图或谱系图）来组织数据。

凝聚式聚类 (Agglomerative Clustering): 自底向上。开始时每个数据点都是一个簇，然后逐步合并最相似的簇，直到所有点合并成一个大簇或达到停止条件。
分裂式聚类 (Divisive Clustering): 自顶向下。开始时所有数据点都在一个簇中，然后逐步分裂最大的簇，直到每个点都是一个簇或达到停止条件。

层次聚类假设簇之间存在层次结构，将样本聚到层次化的簇中，属于硬聚类。（硬聚类：一个样本只能属于一个簇，或簇的交集为空集；软聚类：一个样本可以属于多个簇，或簇的交集不为空集）

3.1 分裂聚类（自上而下）

开始将所有样本分到一个簇；之后将已有类中相距最远的样本分到两个新的簇；重复此操作直到满足停止条件；得到层次化的类别

3.2 聚合聚类（自下而上）

开始将每个样本各自分到一个簇；之后将相距最近的两簇合并，建立一个新的簇；重复此操作直到满足停止条件；得到层次化的类别

四、基于模型的聚类 (Model-based Clustering)

这类算法假设数据是由某种概率分布（如高斯分布）生成的，并尝试找到最能解释数据生成过程的参数。

高斯混合模型 (Gaussian Mixture Model, GMM): 假设数据是由多个高斯分布的混合生成的。它使用期望最大化（EM）算法来估计每个高斯分量的参数（均值、协方差、权重）。

聚类评估指标

由于聚类是无监督的，评估其效果比分类更复杂。

内部评估指标 (Internal Evaluation): 不依赖真实标签，仅根据聚类结果本身来评估。
- 轮廓系数 (Silhouette Coefficient): 衡量一个点与其自身簇的相似度以及与其他簇的相异度。值范围 $[- 1, 1]$ ，越高越好。
- Davies-Bouldin Index: 衡量簇内距离与簇间距离的比率，越低越好。
外部评估指标 (External Evaluation): 需要真实标签来评估聚类结果与真实标签的匹配程度。
- 调整兰德指数 (Adjusted Rand Index, ARI): 衡量两个聚类结果（一个是你算法的，一个是真实标签的）之间的一致性，范围 $[- 1, 1]$ ，越高越好。
- 同质性 (Homogeneity): 每个簇只包含单一类别的样本。
- 完整性 (Completeness): 相同类别的样本都被分到同一个簇中。
均一性： $p$ 类似于精确率，一个簇中只包含一个类别的样本，则满足均一性。也可以认为是正确率 (每个聚簇中正确分类的样本数占该聚簇总样本数的比例和)
完整性： $r$ 类似于召回率，同类别样本被归类到相同簇中，则满足完整性;(每个聚簇中正确分类的样本数占该类型的总样本数比例的和)
V-measure：均一性和完整性的加权平均（ 𝛽 默认为 1）
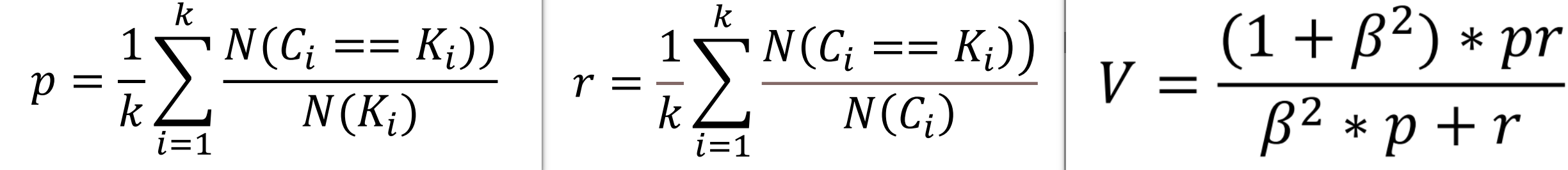
轮廓系数：越接近 1 表示样本 $i$ 聚类越合理；越接近-1，表示样本 $i$ 应该分类到另外的簇中；近似为 0 ，表示样本 $i$ 应该在边界上。簇内不相似度: 计算样本𝑖到同簇其它样本的平均距离为𝑎(𝑖)，应尽可能小。簇间不相似度: 计算样本𝑖到其它簇𝐶𝑗的所有样本的平均距离𝑏𝑖𝑗，应尽可能大。
调整兰德系数 Adjusted Rnd Index： ARI 取值范围为 $[- 1, 1]$ ，值越大意味着聚类结果与真实情况越吻合，衡量的是两个数据分布的吻合程度

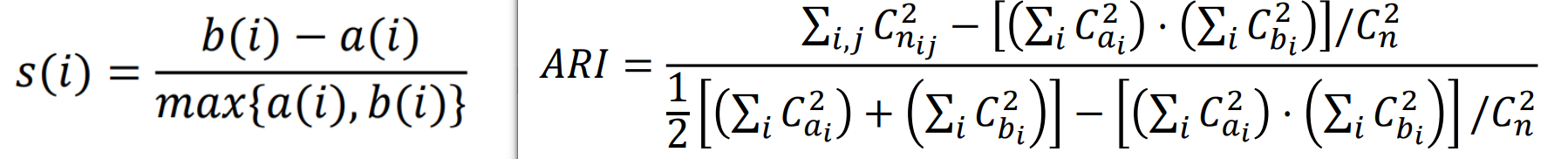
聚类效果示例 (Mermaid)

graph TD
    subgraph 聚类算法效果示意
        A["原始数据 (无标签)"] --> B{K-Means}; 
        B --> C(发现球形簇, 对噪声敏感);
        A --> D{DBSCAN}; 
        D --> E(发现任意形状簇, 识别噪声);
        A --> F{层次聚类}; 
        F --> G(生成树状图, 可视化合并/分裂过程);
    end

    style C fill:#fff,stroke:#333,stroke-width:2px
    style E fill:#fff,stroke:#333,stroke-width:2px
    style G fill:#fff,stroke:#333,stroke-width:2px

使用场景

医疗：使用聚类算法来发现疾病；市场细分：了解用户群，然后对每个客户进行归类；金融业：观察到可能的金融欺诈行为；搜索引擎：聚类的相似结果；社交网络：给朋友进行分组

市场细分、文档聚类、图像分割、图像压缩、聚类分析、特征学习或者词典学习、确定犯罪易发地区、保险欺诈检测、公共交通数据分析、IT 资产集群、客户细分、识别癌症数据、搜索引擎应用、医疗应用、药物活性预测