决策树
Decision Trees
监督学习,判别模型,用于分类和回归问题。分而治之,递归,贪心算法
基于树结构进行决策,从数据特征中推断目标值。
决策树学习的目的:产生一棵泛化能力强(处理未见示例能力强)的决策树
归纳的基本算法是贪心算法(在每一步选择中都采取在当前状态下最好/优的选择),自顶向下来构建决策树。决策树的生成过程中,属性选择的度量是关键。
决策树基本原理
决策树的构建是一个递归的过程,其核心思想是自顶向下、分而治之。在每个节点,算法会选择一个最佳特征来分裂数据,使得分裂后的子集尽可能“纯净”(即同类样本集中,或数值差异小)。这个“纯净度”通常通过信息增益 (Information Gain)、信息增益率 (Information Gain Ratio) 或 基尼不纯度 (Gini Impurity) 等指标来衡量。
分类树的构建过程:
- 从根节点开始,包含所有训练样本。
- 遍历所有特征,计算每个特征在当前节点上进行分裂后的“纯净度”指标。
- 选择能够最大化纯净度提升(或最小化不纯度)的特征作为当前节点的分裂属性。
- 根据选择的特征和其取值,将数据分裂成若干个子集,形成新的子节点。
- 对每个子节点递归地重复上述过程,直到满足停止条件(例如,节点中的样本都属于同一类别,或者达到预设的最大深度,或者样本数量过少)。
回归树的构建过程类似,但衡量纯净度的指标通常是均方误差 (MSE) 或平均绝对误差 (MAE),目标是使得分裂后子节点内样本的输出值方差最小。
建立决策树的关键,即在当前状态下选择哪个属性作为分类依据,根据不同的目标函数,主要有三种算法
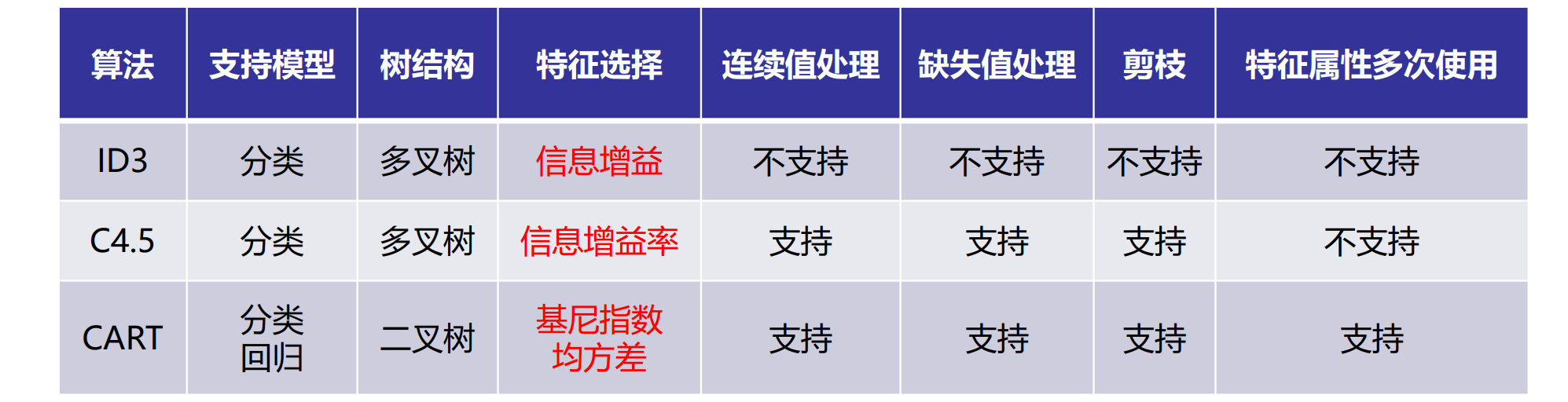
一、 ID3 Iterative Dichotomiser 3
核心:信息熵。以信息增益为衡量标准,选取最高增益的属性作为分类的标准。
期望信息越小,信息熵越大,样本纯度越低
- 使用信息增益作为分裂标准。
- 倾向于选择取值多的特征,可能导致过拟合。
- 只能处理离散型特征。
算法流程
初始化特征集合和数据集合;
计算数据集合信息熵和所有特征的条件熵,选择信息增益最大的特征作为当前决策节点;
更新数据集合和特征集合
重复 2,3 两步,若子集值包含单一特征,则为分支叶子节点
实际计算
- 信息熵:
- 条件熵:
- 信息增益:

缺点
没有剪枝,容易过拟合;只能用于处理离散分布的特征;没有考虑缺失值
二、 C4.5
用信息增益率来选择属性。ID3选择属性用的是子树的信息增益,而C4.5用的是信息增益率;在决策树构造过程中进行剪枝;对非离散数据也能处理;能够对不完整数据进行处理
预剪枝、后剪枝
缺点:C4.5 用的是多叉树,用二叉树效率更高;只能用于分类;使用的熵模型拥有大量耗时的对数运算,连续值还有排序运算;在构造树的过程中,对数值属性值需要按照其大小进行排序;只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时,程序无法运行
- ID3 的改进版,使用信息增益率作为分裂标准,克服了 ID3 倾向于多值特征的缺点。
- 可以处理连续型和离散型特征。
- 引入了剪枝 (Pruning) 机制来防止过拟合。
三、 CART
Classification and Regression Tree
- 目标变量是离散的,称为分类树,基尼指数来选择属性(分类)
- 目标变量是连续的,称为回归树,均方差来选择属性(回归)
- 既可以用于分类也可以用于回归。
- 分类树使用基尼不纯度作为分裂标准。
- 回归树使用均方误差作为分裂标准。
- 总是生成二叉树。
优点与局限性
- 优点:
- 易于理解和解释: 树状结构直观,决策路径清晰可见,被称为“白箱模型”。
- 无需数据预处理: 对缺失值不敏感,不需要对数据进行归一化或标准化。
- 可以处理数值型和类别型数据。
- 能够自动进行特征选择。
- 局限性:
- 容易过拟合: 单个决策树模型容易对训练数据过度拟合,导致泛化能力差。
- 对数据波动敏感: 训练数据的微小变化可能导致树结构发生很大变化。
- 局部最优: 贪婪算法,每次分裂只考虑当前最佳,不保证全局最优。
- 对于某些复杂关系,可能需要非常深的树,导致模型复杂且难以解释。