图

Graph
一种由顶点 (Vertex) 和边 (Edge) 组成的非线性数据结构

一、基础知识

我们可以将图 $G$ 抽象地表示为一组顶点 $V$ 和一组边 $E$ 的集合：如果将顶点看作节点，将边看作连接各个节点的引用（指针），我们就可以将图看作一种从链表拓展而来的数据结构。

相较于线性关系（链表）和分治关系（树），网络关系（图）的自由度更高，因而更为复杂。

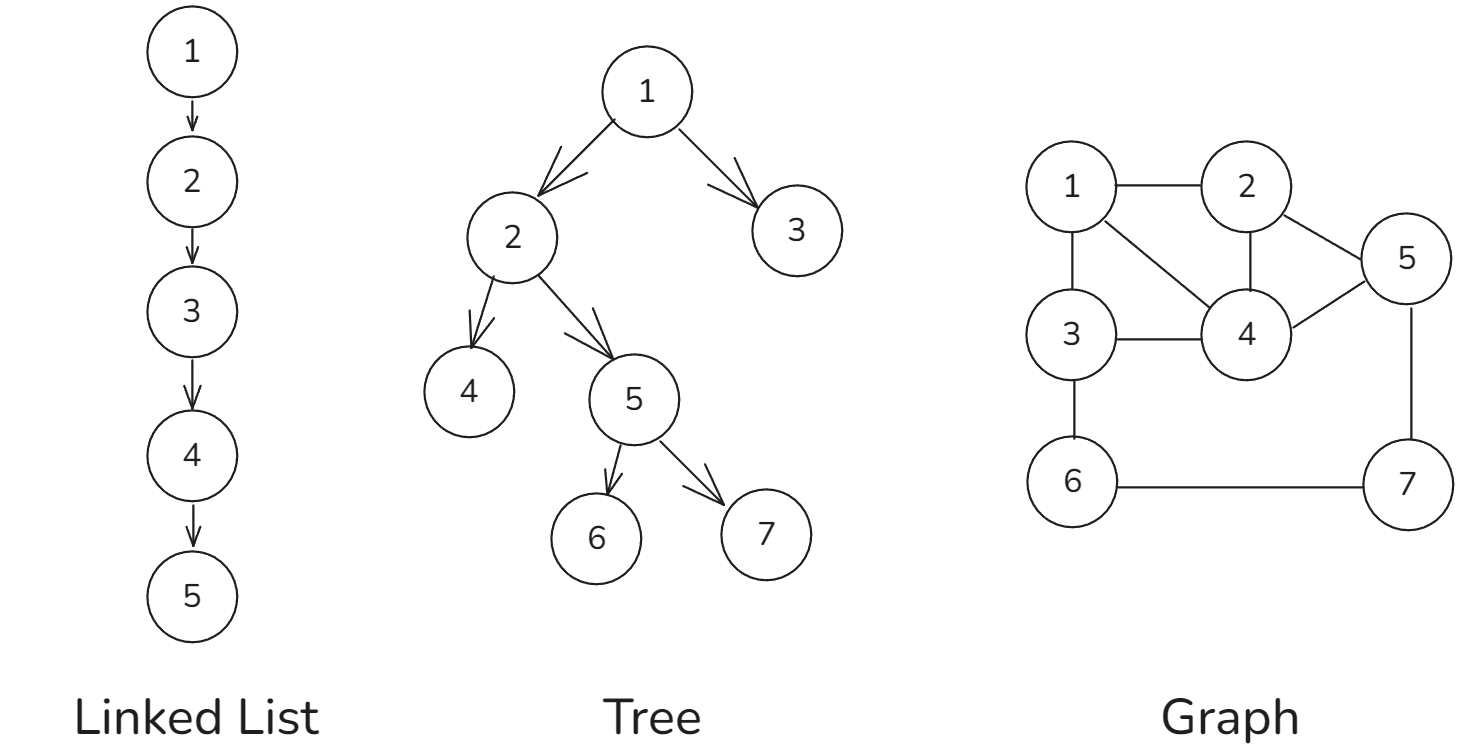
常用术语

邻接（adjacency）：当两顶点之间存在边相连时，称这两顶点“邻接”
路径（path）：从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”
度（degree）：一个顶点拥有的边数。对于有向图，入度（in-degree）表示有多少条边指向该顶点，出度（out-degree）表示有多少条边从该顶点指出。

二、图的常见类型

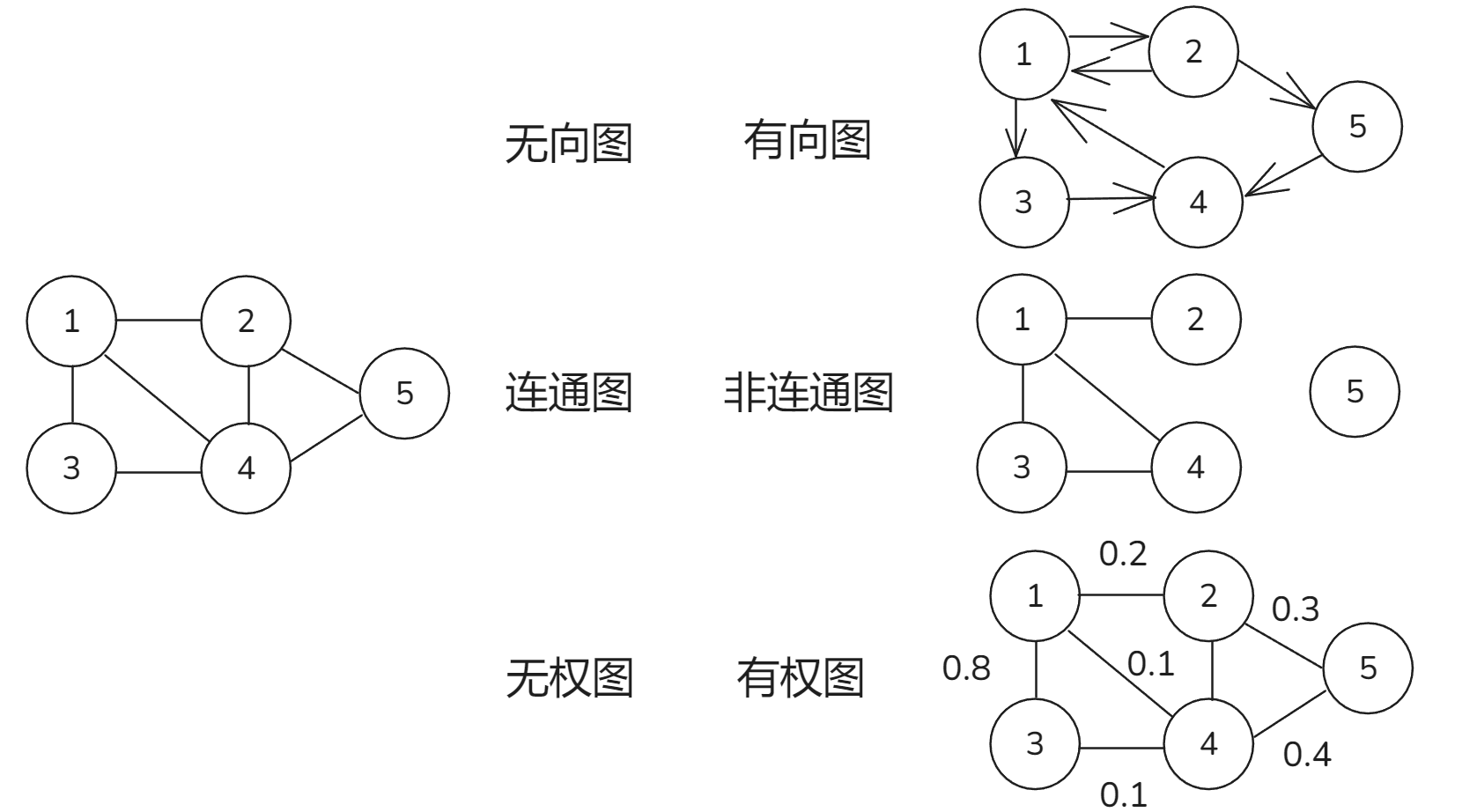
1. 所有顶点是否连通

可分为连通图（connected graph）和非连通图（disconnected graph）：

对于连通图，从某个顶点出发，可以到达其余任意顶点。
对于非连通图，从某个顶点出发，至少有一个顶点无法到达。

2. 边是否具有方向

可分为无向图（undirected graph）和有向图（directed graph）：

在无向图中，边表示两顶点之间的“双向”连接关系
在有向图中，边具有方向性

3. 边是否具有权重

可分为无权图 (unweighted graph) 有权图 (weighted graph)：

有权图：在这种图中，每条边都被赋予了一个数值，这个数值称为"权重"（weight）。权重可以代表两个顶点之间的距离、成本、容量或其他某种意义上的度量。
无权图：与有权图相对，无权图中的边没有赋予任何权重。这意味着图中每条边的价值或成本被视为相同，或者这种信息在当前的问题中并不重要。

三、图的数学表示

对于一个含有 $n$ 个顶点的图 $G = (V, E)$

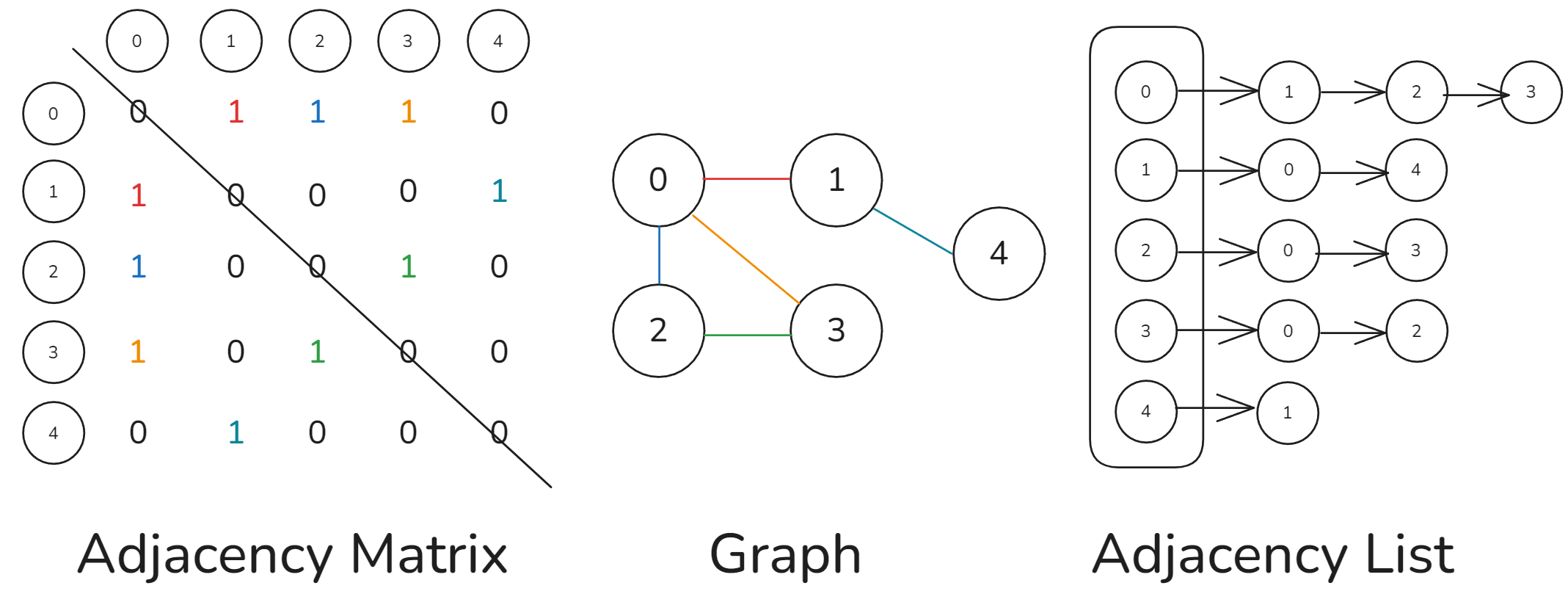
1. 邻接矩阵 Adjacency Matrix

设图的顶点数量为 $n$ ，邻接矩阵使用一个 $n \times n$ 大小的矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，用 1 或 0 表示两个顶点之间是否存在边。

\begin{array}{r} A [i] [j] = {\begin{cases} 1 i f (i, j) \in E \\ 0 e l s e \end{cases} \end{array}

邻接矩阵具有以下特性：

顶点不能与自身相连，因此邻接矩阵主对角线元素没有意义（均为 0）
对于无向图，两个方向的边等价，此时邻接矩阵关于主对角线对称
将邻接矩阵的元素从 1 和 0 替换为权重，则可表示有权图

使用邻接矩阵表示图时，我们可以直接访问矩阵元素以获取边，因此增删查改操作的效率很高，时间复杂度均为 $O (1)$ 。然而，矩阵的空间复杂度为 $O (n^{2})$ ，内存占用较多。

2. 邻接表 Adjacency List

邻接表使用 $n$ 个链表来表示图，链表节点表示顶点。第 𝑖 个链表对应顶点 𝑖 ，其中存储了该顶点的所有邻接顶点（与该顶点相连的顶点）。

邻接表仅存储实际存在的边，而边的总数通常远小于 $n^{2}$ ，因此它更加节省空间。然而，在邻接表中需要通过遍历链表来查找边，因此其时间效率不如邻接矩阵。

A —— B —— C  

A: B  
B: A, C  
C: B

# 无向图
graph = {
    'A': ['B'],
    'B': ['A', 'C'],
    'C': ['B']
}

# 加权图扩展
graph = {
    'A': [('B', 2)],
    'B': [('A', 2), ('C', 3)],
    'C': [('B', 3)]
}

邻接表结构与哈希表中的“链式地址”非常相似，因此我们也可以采用类似的方法来优化效率。

比如当链表较长时，可以将链表转化为 AVL 树或红黑树，从而将时间效率从 𝑂(𝑛) 优化至 𝑂(log⁡𝑛)
还可以把链表转换为哈希表，从而将时间复杂度降至 𝑂(1) 。

四、图的基础操作

主要分为：对“边”的操作和对“顶点”的操作

1. 基于邻接矩阵的实现

以空间换时间

添加或删除边：直接在邻接矩阵中修改指定的边即可，使用 𝑂(1) 时间。而由于是无向图，因此需要同时更新两个方向的边。
添加顶点：在邻接矩阵的尾部添加一行一列，并全部填 0 即可，使用 𝑂(𝑛) 时间。
删除顶点：在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况，需要将 (𝑛−1) 2 个元素“向左上移动”，从而使用 𝑂(𝑛2) 时间。
初始化：传入 $n$ 个顶点，初始化长度为 $n$ 的顶点列表 vertices ，使用 𝑂(𝑛) 时间；初始化 𝑛×𝑛 大小的邻接矩阵 adjMat ，使用 𝑂(𝑛2) 时间。

2. 基于邻接表的实现

以时间换空间

添加边：在顶点对应链表的末尾添加边即可，使用 𝑂(1) 时间。因为是无向图，所以需要同时添加两个方向的边。
删除边：在顶点对应链表中查找并删除指定边，使用 𝑂(𝑚) 时间。在无向图中，需要同时删除两个方向的边。
添加顶点：在邻接表中添加一个链表，并将新增顶点作为链表头节点，使用 𝑂(1) 时间。
删除顶点：需遍历整个邻接表，删除包含指定顶点的所有边，使用 𝑂(𝑛+𝑚) 时间。
初始化：在邻接表中创建 $n$ 个顶点和 2𝑚 条边，使用 𝑂(𝑛+𝑚) 时间。

3. 图的遍历

图的遍历